Понятие лимита широко используется в математике, экономике и программировании. В этой статье мы рассмотрим основные методы нахождения лимитов в различных контекстах.
Содержание
Математические методы нахождения лимита
Лимиты функций
- Прямая подстановка значения
- Разложение на множители
- Использование правила Лопиталя
- Применение эквивалентных бесконечно малых
| Тип функции | Метод решения | Пример |
| Полиномиальная | Прямая подстановка | lim(x→2) (x²+3) = 7 |
| Дробно-рациональная | Разложение на множители | lim(x→1) (x²-1)/(x-1) = 2 |
| Неопределенность 0/0 | Правило Лопиталя | lim(x→0) sin(x)/x = 1 |
Лимиты в экономике и финансах
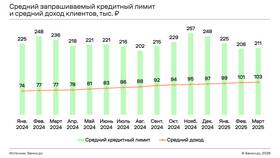
- Кредитные лимиты рассчитываются на основе платежеспособности
- Торговые лимиты определяются рисками
- Бюджетные лимиты устанавливаются планами
Факторы влияния:
- История операций
- Кредитный рейтинг
- Обеспечение
- Рыночные условия
Технические лимиты в программировании
| Тип лимита | Как определяется |
| API-лимиты | Настройками сервера |
| Лимиты памяти | Конфигурацией системы |
| Скоростные лимиты | Пропускной способностью |
Практические примеры нахождения лимитов
Пример 1: Банковский лимит
- Анализ дохода клиента
- Оценка кредитной истории
- Расчет коэффициентов
- Установка границы
Пример 2: Вычислительный лимит
- Тестирование производительности
- Мониторинг ресурсов
- Оптимизация кода
- Установка предельных значений
Важные принципы
- Лимит должен быть обоснованным
- Необходимо учитывать все влияющие факторы
- Лимиты могут динамически изменяться
- Важно предусмотреть механизмы пересмотра
Для точного определения лимитов в конкретной области рекомендуется консультация со специалистами и изучение отраслевых стандартов.