В различных контекстах можно встретить утверждения, начинающиеся со слов "верно ли, что сумма...". Рассмотрим несколько распространенных случаев таких утверждений и их обоснованность.
Содержание
Математические утверждения о сумме
| Утверждение | Верность | Объяснение |
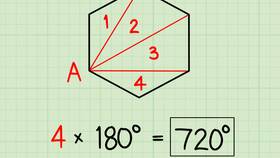
| Верно ли, что сумма углов треугольника равна 180°? | Да | Это фундаментальное свойство евклидовой геометрии |
| Верно ли, что сумма чисел от 1 до n равна n(n+1)/2? | Да | Формула Гаусса для суммы арифметической прогрессии |
| Верно ли, что сумма бесконечного ряда 1+1/2+1/4+1/8+... равна 2? | Да | Пример сходящегося геометрического ряда |
Финансовые утверждения
О страховых суммах
- Верно ли, что сумма страхового возмещения не может превышать страховую сумму? - Да, это основной принцип страхования
- Верно ли, что сумма страховых взносов зависит от риска? - Да, тарифы рассчитываются исходя из вероятности наступления страхового случая
О кредитах и займах
- Верно ли, что сумма ежемесячного платежа включает проценты и часть основного долга? - Да, это характерно для аннуитетных платежей
- Верно ли, что сумма переплаты по кредиту зависит от срока? - Да, чем больше срок, тем больше общая переплата
Юридические утверждения
| Утверждение | Верность |
| Верно ли, что сумма ущерба влияет на квалификацию преступления? | Да |
| Верно ли, что сумма исковых требований ограничена? | Да, в некоторых случаях существуют процессуальные ограничения |
Экономические утверждения
- Верно ли, что сумма ВВП отражает размер экономики? - Да, это основной макроэкономический показатель
- Верно ли, что сумма налоговых поступлений зависит от налоговой базы? - Да, существует прямая зависимость
Логические утверждения
Рассмотрим утверждения о логических суммах:
- Верно ли, что сумма истинного и ложного высказывания дает истину? - Да, в логике дизъюнкции
- Верно ли, что сумма двух отрицаний дает утверждение? - Да, по закону двойного отрицания
Статистические утверждения
- Верно ли, что сумма вероятностей всех исходов равна 1? - Да, это аксиома теории вероятностей
- Верно ли, что сумма отклонений от среднего равна нулю? - Да, это свойство среднего арифметического