Сумма внутренних углов плоского многоугольника зависит от количества его сторон. Для любого n-угольника сумма внутренних углов вычисляется по формуле: (n-2) × 180°, где n - количество сторон многоугольника.
Содержание
Основная теорема о сумме внутренних углов
Примеры для различных фигур
| Фигура | Количество сторон (n) | Сумма внутренних углов |
| Треугольник | 3 | (3-2)×180° = 180° |
| Четырехугольник | 4 | (4-2)×180° = 360° |
| Пятиугольник | 5 | (5-2)×180° = 540° |
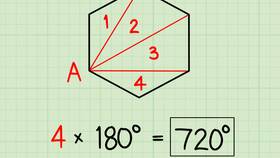
| Шестиугольник | 6 | (6-2)×180° = 720° |
Доказательство формулы
- Выберите одну вершину многоугольника
- Проведите диагонали из этой вершины ко всем несмежным вершинам
- Многоугольник разобьется на (n-2) треугольника
- Сумма углов каждого треугольника равна 180°
- Общая сумма равна (n-2) × 180°
Частные случаи
- Для правильного многоугольника каждый угол равен (n-2)×180°/n
- Сумма углов выпуклого многоугольника всегда равна (n-2)×180°
- Для невыпуклых многоугольников формула также остается верной
Практическое применение
- В архитектуре при проектировании конструкций
- В компьютерной графике при моделировании объектов
- В геодезии при расчетах земельных участков
- В навигации при построении маршрутов
Знание суммы внутренних углов многоугольника является фундаментальным в геометрии и находит применение во многих практических областях. Формула (n-2)×180° позволяет легко вычислять эту сумму для любого плоского многоугольника, независимо от количества его сторон.