Сумма углов является важной характеристикой геометрических фигур, позволяющей определять их свойства и решать различные задачи. В зависимости от типа фигуры и пространства, в котором она рассматривается, сумма углов может иметь разные значения.
Содержание
Основные теоремы о сумме углов
- Сумма углов треугольника на плоскости
- Свойства суммы углов многоугольников
- Особенности сферической геометрии
- Сумма углов в звездчатых фигурах
Сумма углов треугольника
Классическая евклидова геометрия
| Тип треугольника | Сумма углов |
| Произвольный | 180° |
| Прямоугольный | 90° + два острых угла |
| Равносторонний | 3 × 60° = 180° |
Доказательство теоремы
- Провести прямую, параллельную одной из сторон треугольника
- Использовать свойства накрест лежащих углов
- Показать, что три угла при вершине образуют развернутый угол
- Сделать вывод о сумме 180°
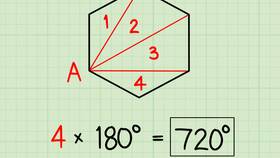
Сумма углов многоугольников
Формула вычисления
Для выпуклого n-угольника сумма углов вычисляется по формуле: (n-2) × 180°
| Фигура | Количество сторон | Сумма углов |
| Четырехугольник | 4 | 360° |
| Пятиугольник | 5 | 540° |
| Шестиугольник | 6 | 720° |
Неевклидовы геометрии
Сферическая геометрия
- Сумма углов треугольника превышает 180°
- Избыток пропорционален площади треугольника
- Пример: на сфере Земли сумма углов может достигать 270°
Гиперболическая геометрия
- Сумма углов треугольника меньше 180°
- Дефект угла зависит от площади фигуры
- Используется в теории относительности
Практическое применение
Примеры задач
- Найти неизвестный угол треугольника по двум известным
- Определить правильность построения многоугольника
- Вычислить параметры сферических фигур в астрономии
- Проверить геометрию конструкций в архитектуре
Важные следствия
- В треугольнике не может быть двух тупых углов
- Сумма внешних углов многоугольника всегда 360°
- Правильные многоугольники имеют равные углы
- В четырехугольнике сумма углов всегда 360°
Знание свойств суммы углов позволяет не только решать геометрические задачи, но и понимать фундаментальные различия между типами геометрий. Эти принципы находят применение в различных областях - от строительства до космологии.